1. 실험 목적
이 실험은 변형률 측정 도구 중에 하나인 Strain gage를 사용하는 방법을 습득하고, 이것을 이용해서 하중이 작용하는 시편에 변형률을 측정하고 모재의 특성을 파악하여 게이지가 부착된 지점의 응력을 계산하고 특히, 이번 실험에서 사용하는 외팔보에서 Strain gage로 측정한 변형률을 이용해서 계산한 응력과 외팔보에 모멘트를 계산해서 얻은 굽힘 응력과 값을 비교해보면서 얼마나 정확한 측정이 이루어지는지 알아보도록 한다.
2. 실험 이론
1. 스트레인 게이지(Strain Gage)
스트레인 게이지, 또는 변형 게이지라고도 하는 이 측정기구는 고체가 변형되면서 고체내의 두 점 사이의 변화량(변형률)을 측정하는 도구이다. 변형률(strain) 이란 어떤 물체가 인장 또는 압축을 받을 때 생기는 변형을 원래 길이로 나눈 값을 말하며, 탄성구간에서 응력과 선형관계를 가지고 그 기울기를 영률(Young's Modulus) 또는 탄성계수(Elastic Modulus) 라고 정의한다. 변형률은 길이를 길이로 나눈 값이기 때문에 따로 차원을 가지지 않고 단위 표기는 [mm/mm] 또는 [in/in]로 한다.


스트레인 게이지에는 종류가 여러 가지 있는데 그중 이번 실험에 사용한 것은 바로 저항식 변형 게이지이다.(그림.1) 이 측정계기는 영국의 물리학자 윌리엄 톰슨(William Thomson)이 발견한 원리를 이용했는데, 이것은 구리선이나 철사와 같은 전도체가 길이가 바뀌거나 압축이 되면 전기저항이 변한다는 것에서 착안한 것이다. 오른쪽 그림과 같이 위에 두 부분이 전선을 잇는 Terminal 부분이고 가운데 발(grid)의 형태로 얇은 전선이 감겨있고 그 위아래로 얇은 2장의 필름으로 덥혀져 있다. 이 필름은 위아래가 구분되어 있으며 반투명한 부분이 위쪽이고 흐릿한 곳이 아래쪽이다. 게이지를 자제에 부착할 때는 이 흐릿한 곳이 붙도록 설치해야한다. 이 기구의 작동원리는 다음과 같이 설명할 수 있다.
이 원리는 앞서 말한 것과 같이 전선의 단면적, 길이의 변화에 따른 전기저항의 변화를 측정하는 것인데, 이 기구를 변형률을 측정하고 싶은 곳에 부착하면 그 지점의 변형만큼 게이지 자체도 같은 비율로 변형이 일어나게 되고 이 변형은 발의 형태로 감겨 있는 전선들도 변형을 하게 만든다. 전기 저항은 다음과 같이 나타낸다.

여기서 비저항은 실험의 변수가 아니므로 스트레인 게이지에서 전기저항은 단면적에 반비례하고 길이에 비례함을 알 수 있다. 즉, 구조의 변형에 따른 스트레인의 변형, 그리고 이어지는 전선의 변형에 의해 게이지의 전기저항이 바뀌는데 이것을 이용해 변형률을 측정할 수 있다. 전기저항과 금속선의 변형률의 관계는 게이지 계수(Gage Factor)로 나타낼 수 있다.
게이지 계수란 금속공학에서 사용하는 용어로 저항선의 변형률 측정에서 전기저항과 변형률의 변화와 비를 변형계의 게이지 계수라고 한다. 이식을 유도하기 위해 저항의 변화량을 구하면

이 식에서 우리가 알고 있는 값은 R(저항), F(게이지계수) 이다. 따라서 변형에 의한 저항의 변화량을 측정한다면 변형률을 구할 수 있게 된다. 우리 실험에 사용된 Strain Gage 는 게이지 계수가 2.1, 그리고 저항이 120 Ohm이였다. 하지만 변형률이라는 것이 워낙 값이 작기 때문에 (변형률인 경우 10^-6) 보통 저항 측정기로는 정확히 측정이 어렵기 때문에 휘스톤 브릿지를 이용해 이 값을 알아보려고 한다. 그럼 휘스톤 브릿지의 원리에 대해서 알아보자.

휘스톤 브릿지란 다이아몬드 철교에서 유래한 이름으로 영국의 물리학자 찰스 휘스톤(Charles Wheatston)이 S.H. 크리스티가 창안한 것을 개량하여 실용화한 전기저항 측정 방법이다. 이것을 사용하는 목적은 첫째로 미지의 저항을 측정할 수 있다는 것과 둘째로 정밀 저항의 측정이 가능하다 는 것이다. 이 구조는 아래 그림과 같이 4개의 저항이 bridge의 형태로 연결되어 있고 그 가운데 검류계가 있다. 그림에서 R2와 R4는 우리가 알고 있는 저항값이다. 그리고 Rv가 가변저항이고 Rx가 우리가 측정하려고 하는 미지의 저항이다. 가변저항을 이용해서 A점과 B점의 전위차를 0으로 맞추면 다음과 같은 식이 성립된다.



로 나타낼 수 있고 미지 저항 Rx의 값을 구할 수 있게 된다.
이제 휘스톤 브릿지가 어떻게 스트레인 게이지에 적용되는지 알아보자. 먼저 R2 대신에 스트레인 게이지에 연결하고(R2=120 Ohm) 구동전압 E를 가했을 때 A점과 B점의 출력전압을 e0라고 하고 e0 = 0 이 되도록 가변저항을 조절하여 Balanced Condition으로 만든다. 이 상황에서 스트레인 게이지가 변형이 되어 저항이 변한다면 브릿지 사이의 전위차가 깨지고( e0 is not 0) 출력전압 측정된다. 그 출력전압을



3. 보의 내력, 모멘트

응력을 구하는 방법이 여러 가지가 있는데 실험에서 측정값과 비교할 이론값으로 굽힘 모멘트를 이용하기 때문에 보의 굽힘 모멘트와 작용하는 응력에 대해서 간단히 알아보자.

보(beam)란 긴 막대가 그 축에 대해 횡방향으로 하중을 받고 있는 구조물을 말하고, 대게 보는 길고, 단면적이 일정한 직선막대를 일컫는다. 보의 종류에도 여러 가지가 있는데 우리가 실험에 사용한 보는 한쪽 끝이 고정된 외팔보(Cantilever) 이다. 수직한 하중을 받고 있는 보에는 보의 내력으로 전단력과 굽힘 모멘트가 작용한다. 보의 각 지점의 단면을 생각해봤을 때 강체의 평형 방정식을 만족하기 위하여 하중 반대방향으로 전단력이 작용하고 그 단면에서 생기는 우력에 대해 자제가 회전하지 않도록 작용하는 모멘트가 굽힘 모멘트이다. 모멘트는 전단력을 적분한 값으로 외팔보와 같은 고정단에서는 하중에다 거리를 곱한 값으로 간단히 나타낼 수 있고 식으로 나타내면

만약 고정단에 작용하는 모멘트를 알고 싶다면 x값에 L을 넣으면 모멘트는 PL이 된다. 이것으로 우리는 스트레인 게이지가 부착된 지점의 모멘트를 이와 같이 구할 수 있다.
그럼 보에 작용하는 모멘트와 응력은 어떤 관계가 있는지 알아보자. 모멘트가 보에 작용하게 되면 보는 작용방향으로 휘게 된다. 그 이유는 아래 그림과 같이 모멘트가 양쪽에서 모일 때는 압축이 일어나고 반대쪽과 같이 모멘트가 벌어지는 쪽은 인장이 일어나게 된다. 이런 수직응력이 보의 내부에서 일어나게 되어 각각의 수직 변형이 일어나는데 이 변형에 따라 보는 휘어지게 되는 것이다. 그리고 이때 작용하는 응력을 굽힘 응력이라고 한다.

굽힘 응력은 다음과 같은 과정에서 유도할 수 있다. 굽혀지는 정도를 곡률로 생각했을 때

즉, 변형률에 이 재료의 탄성 계수를 곱해주면 그 지점의 응력이 된다.
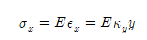
이 응력값은 y에 비례하므로 y값이 커질수록 sigma_x값도 커짐을 알 수 있고 따라서 sigma_max는 y_max인 점에서 발생하게 된다. 그리고 모멘트의 정의에 의해서

로 나타낼 수 있다. 거리제곱을 면적으로 적분한 값은 관성모멘트 I이므로

두 식을 연립하면 최종적으로 모멘트와 모멘트에 의해 발생된 굽힘 응력 간에 관계를 다음 식으로 표현하게 된다.

이 식에서도 마찬가지로 모멘트, M과 관성모멘트, I가 일정한 지점에서 sigma_x는 y에 비례함을 알 수 있다. 특히 y가 중립축으로부터 부재의 높이 거리이기 때문에 위아래의 부호가 다름을 알 수 있고, 그 증가율 역시 그림.8과 같이 선형적으로 변함을 알 수 있다. 이 식을 통해서 보에 작용하는 하중으로 모멘트값을 구하고 스트레인 게이지가 부착된 지점의 이론 응력값을 구할 수 있게 된다.
3. 실험 장치

| 명칭 | 기능 | |
| (1) | Display | 측정되는 값들을 화면에 표시 |
| (2) | Amp zero | 초기값을 0으로 맞춤 |
| (3) | Gage factor | 게이지 계수를 조절 |
| (4) | fine adjustment | 미세하게 조절하는 레버(게이지 계수) |
| (5) | Amp zero | Amp zero 설정 버튼 |
| (6) | Gage factor | Gage factor 설정 버튼 |
| (7) | Balance | 가변 저항값 조절 레버 |
| (8) | fine adjustment | 미세하게 조절하는 레버(밸런스) |
2. 그 외 장비들

4. 실험 방법
| 실험 방법 | |
| (1) | 시편을 사포로 문질러 표면을 매끄럽게 한 후, 알코올로 닦아낸다. |
| (2) | 시편위에 Strain gage와 터미널을 테이프를 이용하여 시편과 수직하게 맞춰 고정한다. |
| (3) | 고정 후 시편위에 테이프가 붙어있던 위치를 표시하고 2/3가량 떼어, strain gage와 terminal에 M-Prep용액을 떨어뜨린다. |
| (4) | 시편위에 테이프가 붙어있던 위치에 본드를 바르고 다시 붙였다 조심스레 뗀다. strain gage와 terminal만이 시편위에 접착된다. |
| (5) | 전선을 납땜하여 고정하고, strain gage와 terminal사이에는 얇은 전선으로 잇는다. |
| (6) | strain gage를 측정하는 장치에 시편을 고정하고 strain indicator와 연결시킨다. |
| (7) | 초기 strain의 값을 0으로 맞춘 후 추의 무게를 증가시켜 stain을 측정한다. |
5. 실험 분석 및 오차
1. 무게-변형률 측정값
다음은 변형률 실험에서 Strain Indicator로 얻어낸 변형률 측정값이다. 휘스톤 브릿지 구조를 통해 계산되는 변형률은 이 기구내부에서 중간계산 되어서 display에서 측정되는 수치가 바로 변형률이다. 실험은 초기 weight 200g 부터 200g 씩 증가시키며 2000g 까지 실험을 진행하였다.
시편 : 알루미늄 6061-T1
| 측정 무게 [ g] | 변형률 [10^-6mm/mm ] | 기타 측정 |
| 200 | 61 | 단면적 : 관성모멘트 : 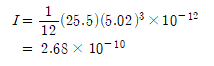 |
| 400 | 127 | |
| 600 | 190 | |
| 800 | 262 | |
| 1000 | 321 | |
| 1200 | 386 | |
| 1400 | 450 | |
| 1600 | 516 | |
| 1800 | 582 | |
| 2000 | 648 |

수치들을 보면 추 200g씩 추가할 때마다 변형률이 약 60씩 증가하는 것을 볼 수 있는데 이것은 시편이 실험 하중 내에서 탄성 변형을 하고 있다는 것을 알 수 있다.
2. 응력, 이론값과 측정값
아래의 표는 무게를 하중으로 나타내고 모멘트를 계산하고, 응력은 실험을 통해 측정한 변형률에 탄성계수를 곱하여 계산한 것이다. 탄성계수는 Matweb홈페이지를 참고하여 시편(Aluminium 6061-T1)의 탄성계수를 정하였고 모멘트는 하중작용 지점으로부터 Strain gage의 중앙지점까지 측정한 거리이다.
| 하중[ N, kgm/s^2] | 모멘트[ Nm] | 변형률 [ 10^-6mm/mm] | 응력[Mpa ] |
| 1.962 | 0.477747 | 61 | 4.148 |
| 3.924 | 0.955494 | 127 | 8.636 |
| 5.886 | 1.433241 | 190 | 12.92 |
| 7.848 | 1.910988 | 262 | 17.816 |
| 9.81 | 2.388735 | 321 | 21.828 |
| 11.772 | 2.866482 | 386 | 26.248 |
| 13.734 | 3.344229 | 450 | 30.6 |
| 15.696 | 3.821976 | 516 | 35.088 |
| 17.658 | 4.299723 | 582 | 39.576 |
| 19.62 | 4.77747 | 648 | 44.064 |

앞의 이론에서 설명했듯이 보의 응력은 모멘트로 구할 수 있으므로 이를 응력 이론값이라고 하고 실험에서 측정한 변형률을 이용해서 계산한 응력 측정값을 비교해본다. 아래표는 이론값과 측정값 그리고 오차와 오차율에 대해서 나타낸 것이고 다음 그래프는 막대그래프로 비교한 것이다.
| 응력(이론값) | 응력(측정값) | 오차 | 오차율(%) |
| 4.47442153 | 4.148 | 0.326422 | 7.295279 |
| 8.94884306 | 8.636 | 0.312843 | 3.495905 |
| 13.42326459 | 12.92 | 0.503265 | 3.749197 |
| 17.89768612 | 17.816 | 0.081686 | 0.456406 |
| 22.37210765 | 21.828 | 0.544108 | 2.43208 |
| 26.84652918 | 26.248 | 0.598529 | 2.229447 |
| 31.32095071 | 30.6 |
0.720951
|
2.301816 |
| 35.79537224 | 35.088 | 0.707372 | 1.976156 |
| 40.26979377 | 39.576 | 0.693794 | 1.722864 |
| 44.7442153 | 44.064 | 0.680215 | 1.520231 |
※ 응력, 오차 단위는 [Mpa]

6. 결 론
1. 실험결과에 대한 평가

이 실험을 준비하면서 몇 가지 주의사항이 있었다. 먼저 부착하고자 하는 곳의 표면이 매끄러워야 했는데, 그 이유는 스트레인 게이지가 10^-6단위의 길이를 측정하는데, 우둘투둘한 표면에 부착되어 있으면 부정확할 수 있기 때문에 부착하기 전에 고운 사포를 이용해서 표면을 매끄럽게 다듬은 후 스트레인 게이지를 부착했다. 그러나 본드를 이용해 붙이는 과정에서 아무리 얇게 펴 바르더라도 결국 미세한 오차는 생길 수밖에 없다. 그러나 실험 결과는 오차는 첫 번째 200g 추를 이용해서 구한 응력에서만 약 7%의 오차가 있었고 그 후로는 4% 미만의 근소한 오차가 발생하여 생각보다 정확한 실험이었다고 평가할 수 있다.
2. 실험을 통해 느낀점
우리는 살아가면서 미세한 변화에 대해 많이 둔감한 편이였다. 아마 중세시대 과학의 선구자들도 그러하지 않았을까하는 생각이 든다. 하지만 물질의 단위가 처음엔 분자에서 원자 나중엔 핵과 전자까지 나뉘어 졌듯이, 우리의 측정 기술도 처음엔 눈대중 단위에서 지금은 첨단기술의 결과물로 나노단위의 물질을 취급하고 있다. 물론 우리가 측정한 단위는 10^-6인 마이크로미터 단위였지만 내가 말하고 싶은 것은 간단한 장비로도 그런 단위를 측정하여 우리가 이론에서 배운 내용을 실험에 적용할 수 있었다는 것이다. 물론 여러 가지 실험이 있었지만 특히 이번 실험에는 전기저항의 특성을 이용해 물리적인 변화를 해석하는 실험이여서 나에게 더욱 뜻 깊었던 것 같다. 앞으로 얼마나 더욱 재밌고 신기한 실험이 기다리고 있을지 모르겠지만, 내가 1학기, 2학기 내도록 배운 재료역학에 대해 좀 더 깊이 알고, 특히 휘스톤 브릿지에 대해 잘 알게 되어서 많은 보람을 느낀 실험이었다.
'공학실험 > 기초공학실험' 카테고리의 다른 글
| 실험6 - 자이로 동특성 실험 (2) | 2023.02.06 |
|---|---|
| 실험4 - 베르누이 정리 실험 (1) | 2023.01.21 |
| 실험3 - 인장강도 측정실험 (0) | 2023.01.20 |
| 실험2 - 회로 및 계측실험 (0) | 2023.01.18 |
| 실험1 - 경도 및 충격시험 (0) | 2023.01.18 |
