1. 실험 목적
이번 실험인 ‘Gyroscope의 동특성 실험’은 Gyroscope운동의 원리를 이해하고 각 방향의 회전운동이 어떤 방향으로 힘이 작용하는지, 그 힘은 얼마나 되는지에 대해 알아보는 실험이었다. 실험은 크게 두가지로 진행하였고, 첫 번째 실험은 Bifilar Pendulum을 이용해서 극관성 모멘트를 측정하는 법을 배우고, 두 번째로 자이로스코프에서 주축의 회전운동과 세차운동으로 인해 발생하는 Gyroscopic Moment를 이해하고 실험적으로 구해본다.
2. 실험 이론
2.1 Bifilar Pendulum
Bifilar는 “두 가닥의 실의“ 정도로 표현할 수 있고 말 그대로 두 가닥의 실을 물체의 양 끝에 달고 물체의 탄성에 의해 진동하는 비틀림 진자이다. 역학적으로 보아 진자는 조금이라도 관성이 있으며, 또한 그 위치가 평형점으로부터 벗어나게 될 때는 그 평형의 위치로 돌아가려는 작용을 하게 되므로, 이 경우의 진동주기는 일반적으로 관성과의 관계에 의하여 주어진다. 자이로스코프 실험에서의 토크 값에 필요한 극관성 모멘트를 구하기 위하여 사용된다.



2.2 오일러 각을 이용한 자이로 운동방정식
1. 오일러 각이란?
: 오일러 각(Euler angle)이란 강체가 놓은 방향을 3차원 공간에 표시하기 위해 레온하르트 오일러가 도입한 세 개의 각도이다. 즉 3차원 공간에 놓인 강체의 방향은 오일러 각도를 사용하여 세 번의 회전을 통해서 얻을 수 있다.
오일러 각은 강체의 3차원 공간 좌표계의 회전으로 이해하는 것이다. 회전된 좌표계의 각도는 다음과 같이 정의된다.
| 오일러 각 | |
| 1. | a : 축을 회전축으로 하여 회전된 좌표축의 각도 |
| 2. | b : 회전된 축을 회전축으로 하여 회전된 좌표축의 각도 |
| 3. | c : 위에서 회전된 축을 회전축으로 하여 회전된 좌표축의 각도 |
위와 같이하여 강체의 방향은 세 개의 각도로 표시될 수 있다. 로봇 제어와 같은 기기 제어에서는 roll, theta, yaw의 표현이 자주 쓰인다. 오일러 각은 강체의 자세를 좌표축의 회전으로 표현하는 여러 가지 방법 가운데 하나로 회전축의 순서에 따라 Z-X-Z 좌표라고도 불린다. 오일러 각 이외에 강체의 자세를 표현하는 방법으로는 좌표계 (X, Y, Z)에 대해 X축의 회전을 롤(roll), Y축 회전을 피치(pitch) 그리고 Z축의 회전을 요(yaw)이라고 표기하는 좌표가 있다.
2. 자이로 운동방정식

강체의 회전은 크게 고정점에 대한 회전운동, 대칭/ 비대칭의 평면운동, 3차원 공간운동으로 나눌 수 있다. 그중에서 자이로스코프의 운동이 회전축의 방향과 각운동량의 방향이 일치하지 않는 3차원 공간운동을 말한다.
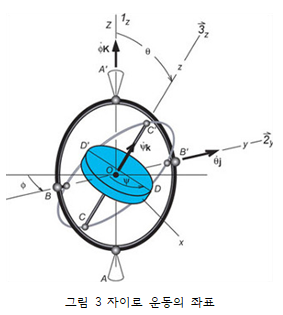
일반적인 강체의 회전을 정의하기 위해서 3차원의 공간운동에서 고정좌표계에 대한 회전을 생각할 수 있는데, 회전축이 고정되어 있지 않으므로 ‘세차운동’에 의해 회전축이 회전하게 된다. 만약 고정좌표에서 이를 해석한다면 Ix, Iy, Iz 가 모두 W_gxyz에 대한 미분을 받으로 상당히 복잡하게 해석된다. 따라서 우리는 회전축을 관성주축으로 선정하여 관성모멘트가 일정한 값을 가지는 회전좌표계를 도입해서 보다 간단하게 방정식을 세울 수 있다. <그림.3>에서 회전좌표계의 G-xyz 를 관성주축으로 설정하고 원점에 대한 각운동량을 계산해보면

라고 나타낼 수 있다. 여기서 Ix, Iy, Iz는 원점에 대한 회전좌표계의 관성 모멘트이다. 이때 자이로의 운동방정식은

이며 좌표계의 각속도 Omega를 자이로의 각속도 w와 같다고 (물체에 부착) 가정하면

cross벡터 연산하고 각 성분별로 정리하여 표현하면

로 정의하고 이 식들을 오일러 방정식이라고 한다. 이 식을 가지고 자이로스코프의 운동을 기술할 수 있으며 자이로의 해석을 통해서 일상생활에 이용할 수도 있다.

정상세차운동에 대해서 알아보자. 우측에 <그림.4> 과 같은 자이로스코프 운동이 있다고 하자. 차축을 회전시켜 A점을 놓으면 팽이는 세차운동(P점을 중심으로 원운동)을 하게 된다. 그러나 세차운동과 함께 작은 연직운동도 동시에 일어나는데 이를 장동(Nutation)이라고 한다. 그리고 세차운동이 일어날 때 장동운동이 일어나지 않는 것을 정상세차운동이라고 한다.
우선 식을 전개하기 위해 좌표를 <그림.5>와 같이 정의하자. 그러면 우리가 실험에서 무게추를 달아 발생하는 모멘트는 x방향으로 작용하고, 식으로 나타내면

이렇게 나타낼 수 있다.

주축은 z축을 중심으로 wp의 각속도로 회전하고 세차축은 y축을 중심으로 w의 각속도로 회전한다. 세차축에 의해서 발생되는 각운동량을 T라고 하자. 각운동량은 관성모멘트와 각속도의 곱으로 나타내기 때문에 다음과 같이 나타낼 수 있다.

세차축은 주축의 회전운동에 의해서 z축으로 회전한다. 미소시간 dt동안에 움직여서 dtheta만큼 움직였다고 하자. 물론 정상세차운동이므로 z축방향의 연직운동은 없다. 시간에 따라 각운동량의 변화량을 t 라고 한다면 아래와 같이 나타낼 수 있다. T의 크기는 일정한 각 운동량에 의해 고정되나 방향이 계속 바뀌기 때문에 theta의 함수가 되므로 chain rule을 이용해서 식을 전개한다.

시간에 대한 theta의 변화량은 주축의 각속도 이고 위에 전개한 T를 대입하면

Ip와 w는 상수이므로 반지름방향의 단위 벡터 er 을 theta에 대해 미분을 하게되면

세차축의 각운동량의 미소 시간에 대한 각운동량은 r방향의 수직인 theta방향으로 Ipwwp만큼의 모멘트가 생기게 된다. 만약 x-y평면이 지면과 평행하다면 무게추로 입력하는 모멘트와 일치하므로

이와같이 각속도와 관성모멘트에 의해 측정되는 모멘트와 무게추에 의해 발생되는 모멘트의 관계식을 도출할 수 있다.
앞절에서 설명한 일반적인 자이로의 운동에서도 이와같은 식을 유도할 수 있다. 먼저 이 자이로스코프는 r방향과 z방향의 회전이 있는데 r방향의 회전을 y로 고정하면 wx = 0이 되고, 각 방향의 각속도는 일정하게 조절하므로 각가속도는 모두 0이 된다. 그러면

즉, x성분(r방향의 수직인 theta성분)의 모멘트만 남게 되고 Ix가 Iy에 비해 무시할 만큼 작다고 한다면

이렇게 나타낼 수 있다. 이식을 위에서 유도한 식과 비교해본다면
축 방향의 관성모멘트와 각속도는 세차축을 의미하고 z축 방향의 각속도는 주축을 의미한다. 그리고 (-)부호는 <그림.5>에서 봤을 때 앞으로 나오는 방향이 x의 양의방향이고 r의 방향은 x의 음의 방향이기 때문에 위 모멘트식이 바로 앞에서 구한
식과 일치하는 것을 알 수 있다.
3. 실험 방법
3.1 Bifilar Pendulum을 이용한 극관성 모멘트 측정
| Bifilar Pendulum | |
| (1) | Bifilar Pendulum의 실의 길이를 측정한다. |
| (2) | 추의 임의의 각도( theta<<1)만큼 회전 시킨 후 추를 놓아서 10회 왕복시의 시간을 측정한다. |
| (3) | 공식에 위의 회전수를 대입해서 극관성 모멘트( Ip )를 구한다. |
3.2 Gyroscopic Moment 측정
| Gyroscopic Moment | |
| (1) | Gyroscope에 무게추를 부착한 후 주축을 일정한 각속도로 회전시킨다. |
| (2) | 세차운동 각속도를 조절해서 Gyroscopic Couple상태(평형상태)로 만든다. |
| (3) | Gyroscopic Couple상태에서의 주축 및 세차운동 각속도를 측정한다. - 주축운동의 각속도는 Front Panel상의 Dial 버튼을 이용 측정/변경 가능하다. |
| (4) | 부가 무게를 바꿔가며 (1)~(3)단계를 반복한다. |
| (5) | 부가모멘트를 계산해서 이론상의 값으로 하고, 실험으로 구한 Gyroscopic Moment( t )와 비교해본다. |
4. 실험 결과 Data 및 오차 분석
4.1 Bifiler Pendulum을 이용한 극관성 모멘트 측정
| h(mm) | D(mm) | m(g) | T(sec) | n(rev) | (Hz) |
| 550 | 65 | 367.5 | 8.4 | 10 | 1.190476 |

실험 방법대로 Bifilar Pendulum에 두 개의 실을 고정하여 총 10번의 주기운동의 시간을 측정하였다. 따라서 평균 1회 왕복운동의 시간은 0.84초였고 그 진동수는 1.190476Hz가 나왔다. 이 진동수를 가지고 Bifilar Pendulum의 원리에 의해 정의된 식에 대입해서 세차축에 이용된 회전판의 극관성 모멘트를 구할 수 있었다. 식에 대입해서 구한 극관성 모멘트는 123.745e-6 kgm^2이 나왔다. 이 극관성 모멘트 값을 이용해서 모멘트 변화량에 의해 생기는 Gyroscopic Moment의 값을 구해보고 또 이론적인 Moment를 이용해서 극관성모멘트를 역으로 계산하고 오차를 구해본다.
4.2 Gyroscopic Moment의 측정 data


실험 결과를 보면 추의 무게가 증가할수록 즉, 작용하는 모멘트가 클수록 입력하는 각속도가 증가하는 것을 볼 수 있고 주축의 각속도가 커지면 세차축의 각속도가 작아지고 주축의 각속도가 작아지면 세차축의 각속도가 커지는 반비례관계를 볼 수 있다. Bifilar Pendulum을 이용해서 구한 극관성 모멘트와 실험에 제어변수였던 주축의 각속도와 세차축의 각속도를 이용해서 Gyroscopic Moment를 계산했고 그 반대편에는 무게추를 이용해서 부가한 모멘트와 평형을 이루게 조절해서 정상세차운동을 하게 했다. 그 이론값 모멘트와 측정 모멘트와의 오차율은 20%안으로 우려했던 것 보다 정확하게 나왔다. 가장 정확하게 측정된 값은 오차율이 -1.66%이며 이때 측정된 극관성 모멘트도 실제 극관성 모멘트와 가장 근접하는 값을 가졌다.

각각의 각속도 값은 대체적으로 실험값이 이론값보다 높게 측정되었다. 전체적으로 그래프는 좌 상단에서 우 하단으로 내려가는 반비례하는 성향으로 눈으로 확인할 수 있다. 그리고 무게가 늘어날수록 같은 주축의 각속도를 비교해봤을 때 세차운동이 커지는 양상을 볼 수 있다. 앞서 내용을 전개한 Gyroscopic Moment를 계산할 때 식을 생각해보면 충분히 예상할 수 있는 결과이다.
6. 자이로의 사용 사례

닌텐도의 Wii의 기본 controller이다. Wii와 블루투스로 통신을 하는데 윈도우나 Mac, Linux에도 연결해서 리모컨이나 게임 컨트롤러로 사용할수 도 있다. 내부에 100Hz로, 최대 4개까지의 적외선 광원을 추적할 수 있는 해상도 1024*768의 infra-red camera, 8-bit 해상도의 가속도 센서, 디지털 조이스틱 등을 가지고 있다.
3축 가속도 센서 덕분에 X, Y, Z축에 대한 가속도를 측정할 수 있다. 그리고 자이로를 통해서 pitch, yaw, roll 값도 측정할 수 있는데 이것은 직접 측정한 것은 아니고 가속도 센서 측정값을 조합해서 계산해 낸 값으로 대략의 approximation값이라고 생각해야 한다. 이 문제를 해결한 것이 바로 'Motion Plus'이다.
Motion Plus는 가장 최근에 발표한 Wii용 주변기기이다. mote뒤에 꼽는 adapter형태로 intellisense 의 IDE-650 2축 MEMS Gyroscope sensor(자이로센서)가 들어갔다.

자이로 센서를 세 개 포함시킴으로서 단순한 좌표뿐만 아니라 움직이는 방향을 향하는 힘이나 속도 등도 체크할 수 있게 됨으로서 이전에 비해서 훨씬 섬세하고 자세한 움직임 값을 얻을 수 있게 되었다.
'공학실험 > 기초공학실험' 카테고리의 다른 글
| 실험5 - 변형률 측정 실험 (0) | 2023.01.26 |
|---|---|
| 실험4 - 베르누이 정리 실험 (1) | 2023.01.21 |
| 실험3 - 인장강도 측정실험 (0) | 2023.01.20 |
| 실험2 - 회로 및 계측실험 (0) | 2023.01.18 |
| 실험1 - 경도 및 충격시험 (0) | 2023.01.18 |